- PDF - 11 kio
Personal page of Denis Basko
My research activities
- Theory of superconducting nanostructures
- Anderson localization with interactions
- Optics of two-dimensional materials
- Energy transfer in nanostructures
Collaborators :
theoretical, experimental, post-docs, Ph.D. students, undergraduate students
Teaching
A short CV
Research activities
Theory of superconducting nanostructures
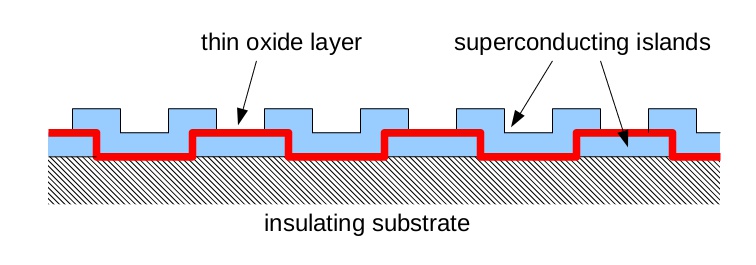
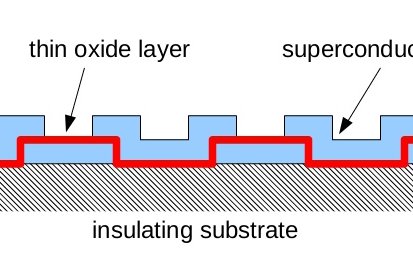
In low-dimensional structures, the superconducting phase excitations (which are nothing else than the plasma oscillations) are gapless, in contrast to bulk superconductors, where the plasma frequency is finite (and usually quite high, a few eV). Thus, in low-dimensional structures at temperatures well below the superconducting gap (which is typically a few Kelvins) the dominant role is played by the phase excitations because the quasiparticles are frozen out. I am interested in the effect of spatial inhomogeneity on the phase excitations and its consequence for various physical phenomena which involve phase excitations (such as quantum phase slips). I closely collaborate on this topic with several experimental groups at the Néel Institute.
My selected publications on this topic :
D. M. T. van Zanten, D. M. Basko, I. M. Khaymovich, J. P. Pekola, H. Courtois, and C. Winkelmann , "Single Quantum Level Electron Turnstile ", Physical Review Letters 116, 166801 (2016).
M. Taguchi, D. M. Basko and F. W. J. Hekking, "Mode engineering with a one-dimensional superconducting metamaterial ", Physical Review B 92, 024507 (2015).
D. M. Basko and F. W. J. Hekking, "Disordered Josephson junction chains : Anderson localization of normal modes and impedance fluctuations", Physical Review B 88, 094507 (2013).
Some general reading on this topic :
Anderson localization in the presence of interactions or nonlinearities
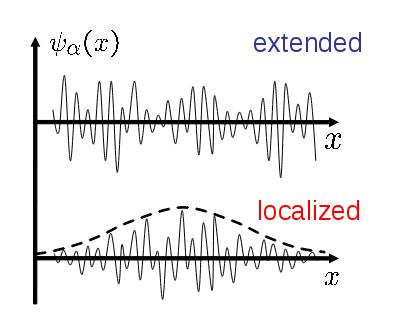
Anderson localization is a universal phenomenon, not specific to electrons in disorder. It has been observed for microwaves, light, acoustic waves, and ultracold atoms. It may occur for any wave trying to propagate through a disordered medium. Quantum mechanics is only needed to make particles behave like waves. Formally, one always studies eigenfunctions of a linear operator which contains Laplacian of some sort (differential or discrete), as well as some kind of disordered potential.
Anderson localization is reasonably well understood for non-interacting particles or linear waves. For nonlinear waves the superposition principle breaks down completely ; for interacting quantum particles it holds, but only in the many-body Hilbert space whose dimensionality is exponentially large compared to that of the single-particle problem. Thus, the formal set-up of the problem is completely different from the non-interacting/linear case. Moreover, it depends on the specific system. A relatively simple case is when the system is coupled to an external thermal bath (e. g., electrons coupled to phonons). The bath provides noise which destroys coherence, necessary for Anderson localization. Then the localization is destroyed, and transport is allowed. But what happens if there is no external bath, just intrinsic interaction between particles or nonlinearity present in the medium ? Will the particles be able to propagate ?
My fascination with the subject comes from the very basic question, underlying the whole statistical physics : how does a system, governed by the reversible Hamiltonian dynamics (whether classical or quantum), irreversibly reach the thermal equilibrium ? Indeed, a localized non-interacting/linear system never equilibrates : the particles will simply sit in their localized states forever. It is only interaction/non-linearity that may (or still may not) lead to non-trivial kinetics, which results in equilibration and transport. Besides this fundamental interest, the problem is quite challenging from the technical point of view, and requires development of new theoretical tools.
My selected publications on this topic :
D. M. Basko, "Weak chaos in the disordered nonlinear Schrödinger chain : destruction of Anderson localization by Arnold diffusion", Annals of Physics 326, 1577–1655 (2011).
D. M. Basko, I. L. Aleiner, and B. L. Altshuler, "Metal-insulator transition in a weakly interacting many-electron system with localized single-particle states ", Annals of Physics 321, 1126–1205 (2006).
Some general reading on this topic :
(Magneto-)optics of graphene and other two-dimensional materials
Electrons in such materials are most often probed either by transport measurements (i.e., one attaches contacts to the sample and measures current), or by optical spectroscopy (one shines light on the sample and analyzes the light that comes out). Absorption spectroscopy (measurement of how much light is lost in the sample) probes excitations of the crystal with energies corresponding to that of the incident photons. typically, electron-hole pairs. Raman spectroscopy (measurement of how much light comes out at frequencies different from the incident frequency) probes excitations at lower energies, and can detect electronic excitations, as well as phonons. Raman spectroscopy can also give information on electron-phonon coupling.
Application of a magnetic field to the sample provides an additional degree of freedom for probing electronic properties. Indeed, instead of the continuous band, electronic spectrum in two-dimensional systems shrinks into a sequence of discrete Landau levels, so all optical transitions are modified. Magneto-absorption and magneto-Raman measurements detect how exactly they are modified, and provide additional information on electrons, phonons, and their interactions.
In order to interpret the measurement results and extract the useful information, one needs a good theoretical understanding of the optical properties. Two-dimensional materials often have quite simple structure with high symmetry, so that many phenomena can be described by simple models whose parameters are well known and calculations can often be done all the way to final numbers which can be compared to experiments. Indeed, I have benefited a lot from collaborations with experimental groups of Marek Potemski at the Laboratoire National des Champs Magnétiques Intenses in Grenoble and of Andrea Ferrari at the Department of Engineering in Cambridge University.
My selected publications on this topic :
C. Faugeras, S. Berciaud, P. Leszczynski, Y. Henni, K. Nogajewski, M. Orlita, K. Watanabe, C. Forsythe, P. Kim, A. K. Geim, D. M. Basko, M. Potemski, " Landau level spectroscopy of electron-electron interactions in graphene ", Physical Review Letters 114, 126804 (2015) .
D. M. Basko, "Theory of resonant multiphonon Raman scattering in graphene", Physical Review B 78, 125418 (2008).
Some general reading on this topic :
"Optical properties of atomically thin transition metal dichalcogenides : observations and puzzles",
Nanophotonics 6, 1289 (2017).
A. C. Ferrari and D. M. Basko, "Raman spectroscopy as a versatile tool for studying the properties of graphene", Nature Nanotechnology 8, 235 (2013).
K. S. Novoselov, "Nobel Lecture : Graphene : Materials in the Flatland, Reviews of Modern Physics 83, 837 (2011).
Energy transfer in nanostructures
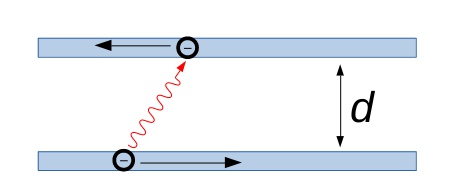
When two small objects are separated by a few nanometers, their electronic excitations can couple to each other via Coulomb interaction even in the absence of any electric contact. Thus, even if the charge transfer between the two objects is completely blocked, the energy can still be transferred. This can be viewed as an electron-electron collision where the two electrons resides on different parts of the structure. When the spatial separation is not too small, such process can go via emission and reabsorption of a photon. If the separation is much smaller than the photon wavelength at the relevant frequency, it is the instantaneous Coulomb interaction that dominates the process. Because electric contact is not required for this processes, the two subsystems can be of of the same or of quite different physical nature : two organic molecules (Forster transfer), two pieces of metal, a semiconductor and an organic material.
I find energy transfer fundamentally interesting because it is a purely interaction effect, it cannot be described in a model of non-interacting electrons. From the practical point of view, it may be used to pump energy between different parts of the structure. Conversely, it may be an important mechanism of unwanted heat leakage at low temperatures, when phonons are frozen out.
My selected publications on this topic :
D. M. Basko, F. Bassani, G. C. La Rocca, and V. M. Agranovich, "Electronic energy transfer in a microcavity", Physical Review B 62, 15962–15977 (2000).
D. Basko, G. C. La Rocca, F. Bassani and V. M. Agranovich, "Förster energy transfer from a semiconductor quantum well to an organic material overlayer", European Physical Journal B 8, 353–362 (1999).
Some general reading on this topic :
A. I. Volokitin and B. N. J. Persson, "Near-field radiative heat transfer and noncontact friction", Reviews of Modern Physics 79, 1291–1329 (2007).
Present and former collaborators
Theory
Our laboratory : F. W. J. Hekking†
Forschungszentrum Jülich : G. Catelani
University of Wisconsin : M. G. Vavilov
Columbia University : I. L. Aleiner, B. L. Altshuler
Landau Institute : M. A. Skvortsov
ICTP Trieste : V. E. Kravtsov
University of Rochester : E. M. Conwell†
Scuola Normale Superiore : F. Bassani†, G. C. La Rocca (my Ph. D. supervisors)
Institute of Spectroscopy : V. M. Agranovich (my Master and Ph. D. supervisor), O. A. Dubovsky, A. M. Kamchatnov (my Master supervisors)
Experiment
Néel Institute : O. Buisson, H. Courtois, W. Guichard, N. Roch, C. Winkelmann
Grenoble High Magnetic Field Laboratory : C. Berthier, C. Faugeras, M. Hirata, M. Orlita, M. Potemski
University of Strasbourg : S. Berciaud
Aalto University : J. Pekola
University of Warsaw : P. Kossacki
Cambridge University : A. C. Ferrari, S. Piscanec
Lebedev Physical Institute : O. P. Varnavsky, A. G. Vitukhnovsky
Post-docs
A. O. Slobodeniuk (2015-)
I. M. Khaymovich (2015-2016)
A. S. Vasenko (2013-2014)
Ph.D. students
J. Wise (ongoing @ University Grenoble-Alps)
A. E. Svetogorov (2019 @ University Grenoble-Alps)
P. Adamus (@ Masaryk University, supervisor D. Munzar, co-supervision with M. Holzmann)
M. Taguchi (2015 @ Unuiversity of Tsukuba, supervisor Y. Tokura, co-supervision with F. Hekking)
F. Pellegrino (2012 @ University of Catania, supervisor G. G. N. Angilella)
Undergraduate students
F. Pfeiffer (2018, University of Konstanz, co-supervision with M. Holzmann)
E.-O. Eljaouhari (2016, University of Tours, co-supervision with F. Hekking)
O. Ly (2014, University of Starsbourg)
G. Crisan (2013, University of Cluj-Napoca, co-supervision with F. Hekking)
Teaching
Kinetic theory and its applications to electron transport in metals
Electronic transport in disordered systems
Electrons in disordered low-dimensional systems
Short CV
2007–2008 : Scuola Internazionale Superiore di Studi Avanzati, Condensed Matter Theory Sector, researcher
2005–2007 : Columbia University, Department of Physics, postdoc
2004–2005 : Princeton University, Physics Department, postdoc
2002–2004 : International Centre for Theoretical Physics, Condensed Matter and Statistical Physics Section, postdoc
2001–2002 : University of Rochester, Chemistry Department, post-doc
1998–2000 : Scuola Normale Superiore di Pisa, Classe di Scienze, Ph.D. student
1991–1997 : Московский физико-технический институт (Moscow Institute for physics and technology), факультет общей и прикладной физики, 126 группа, undergraduate student